Unveiling the Magic of Real Numbers: A Journey through Their Properties
- supriyamathtutor
- Jun 30, 2024
- 4 min read
Hello, budding mathematicians! Today, we're diving into a fascinating topic that forms the bedrock of all the math you'll encounter in your studies: the properties of real numbers. Whether you're calculating your allowance, measuring ingredients for a recipe, or planning a trip, real numbers are everywhere! Understanding their properties can make math not only easier but also much more interesting. Let's explore these properties together.

Before Exploring the Properties, Let's Briefly Understand the Concept of Real Numbers
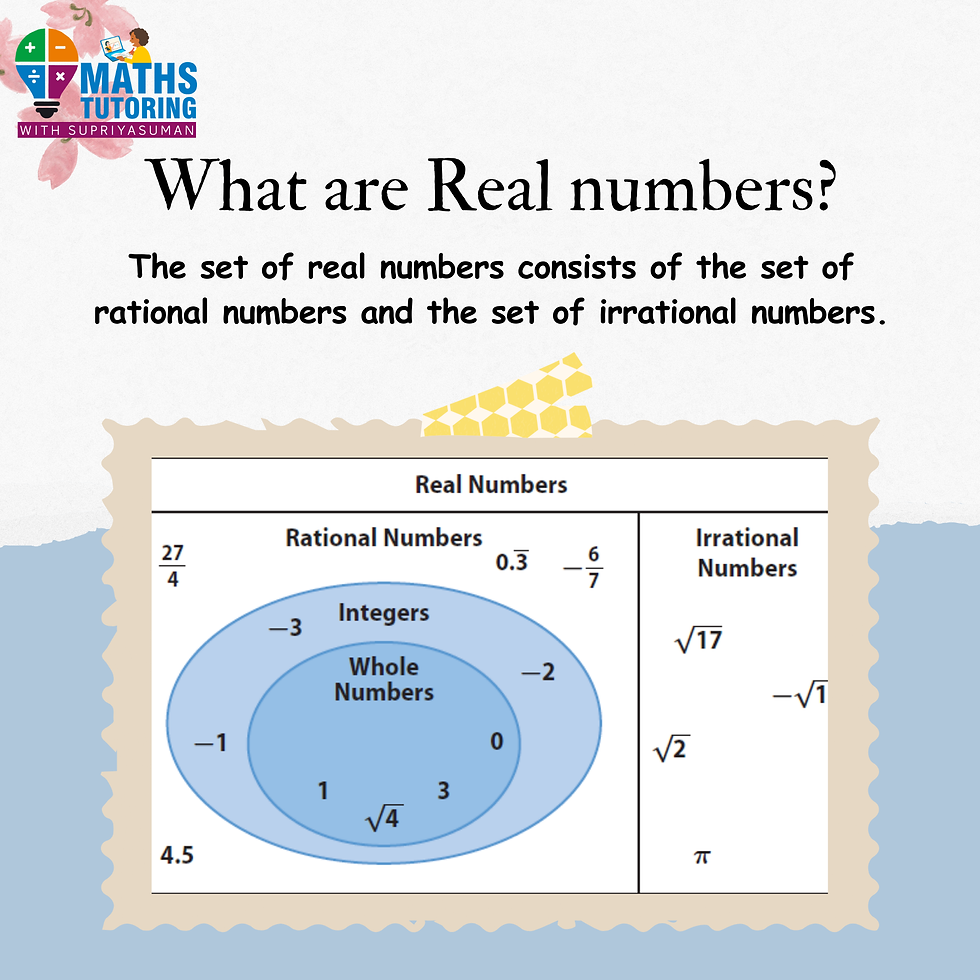
Real numbers are a fundamental part of our everyday lives, even if we don't always realize it. Real numbers are ubiquitous in everyday life, from counting money to measuring distances. Natural numbers are used for counting discrete items, such as the number of people in a room or the quantity of items on a shelf. Whole numbers, including zero, are essential for tasks like tallying inventory or tracking scores. Integers, which include negative numbers, help describe situations involving debt or temperature changes. Rational numbers, expressed as fractions, are used in cooking recipes or calculating financial percentages. Irrational numbers,like π and √2,describe quantities such as the circumference of a circle or the diagonal of a square.Together, these types of real numbers provide a comprehensive framework for quantifying and understanding the world around us.

In essence,real numbers include all the numbers you encounter regularly:
Real numbers can be positive, negative, or zero, making them incredibly versatile for representing continuous quantities. They form the backbone of mathematics and are crucial for solving real-world problems.
Having this basic comprehension of real numbers, let's explore their intriguing characteristics that render them essential in mathematics and beyond!
The Commutative Property: Order Doesn't Matter!
The commutative property states that the order in which two numbers are added or multiplied does not change the result. This property can be expressed mathematically as:
Addition: This is the commutative property of addition: a+b=b+a.
Multiplication:This is the commutative property of multiplication: a×b=b×a.



Understanding the commutative property can make everyday tasks more manageable. Whether you’re budgeting, cooking, or planning an event, knowing that the order of addition or multiplication doesn't affect the outcome can help streamline your processes and reduce errors.
Next time you’re faced with a math problem, remember the commutative property and see how it can simplify your calculations. By rearranging numbers to suit your needs, you’ll find math to be more intuitive and less daunting, paving the way for greater confidence and
The Associative Property: Grouping Doesn't Matter!
The associative property is a fundamental principle in mathematics that plays a crucial role in simplifying and understanding arithmetic operations. This property allows us to regroup numbers when adding or multiplying without changing the result, making complex calculations more manageable. Let's explore the associative property and see how it applies in real-world situations to make math easier and more intuitive.



The Distributive Property: Spreading the Love!
The distributive property states that multiplying a number by a sum (or difference) is the same as multiplying the number by each addend (or minuend and subtrahend) separately and then adding (or subtracting) the results. Mathematically, it is expressed as:
Addition - a×(b+c)=(a×b)+(a×c)
Or for subtraction:
a×(b−c)=(a×b)−(a×c)
The distributive property simplifies complex arithmetic and algebraic expressions, making it easier to solve problems quickly and efficiently. It help us break down and understand larger problems by distributing operations over sums or differences. So next time you’re faced with a tricky math problem, remember the power of distribution and make your calculations a breeze!

The Identity Property: The Unsung Hero of Simplifying Math
The identity property is a fundamental concept in mathematics that helps simplify arithmetic operations. It ensures that numbers retain their original value when combined with specific identity elements. This property applies to both addition and multiplication and plays a crucial role in maintaining consistency in mathematical calculations. Let’s dive into the identity property and explore its significance with real-world examples.



Understanding the identity property is fundamental to mastering algebraic concepts. It forms the basis for more advanced operations and manipulations of equations. By recognizing how numbers behave under addition and multiplication, students can solve equations more efficiently and tackle more complex algebraic problems with confidence.
The Inverse Property: Canceling Out!
In mathematics, the inverse property is a powerful concept that allows us to undo operations, providing a fundamental tool for solving equations and understanding relationships between numbers. Whether in addition and subtraction or multiplication and division, the inverse property enables us to reverse operations and restore original values. Let's explore this essential mathematical principle and its practical applications through real-world examples.



As we conclude our journey through the properties of real numbers, it’s clear that these fundamental concepts are more than just abstract mathematical rules. They are the building blocks of arithmetic and algebra that help us make sense of the world around us. From the commutative property that lets us reorder numbers without changing results, to the distributive property that breaks down complex expressions into simpler parts, each property plays a crucial role in both theoretical and practical applications.
The associative property helps us regroup numbers to make calculations easier, while the identity property introduces us to the special numbers that keep our values unchanged. And don’t forget the inverse property, which allows us to reverse operations and solve equations efficiently.
These properties are not just academic concepts—they are tools that empower us in everyday life. Whether you’re balancing a budget, planning an event, or solving a challenging math problem, these properties offer strategies to simplify and solve problems with confidence.
So next time you dive into a math problem or approach a real-world challenge, remember these properties and how they can help you. Embrace the beauty of these mathematical principles and see how they make the complex simple and the unknown knowable.
Mathematics is like a vast, intricate puzzle, and understanding these properties equips you with the pieces you need to complete it. By mastering these properties, you open doors to new insights and solutions, transforming mathematical challenges into opportunities for learning and growth.
Thank you for joining me on this exploration of the properties of real numbers. Keep practicing, keep exploring, and most importantly, keep enjoying the wonderful world of math!








Comments